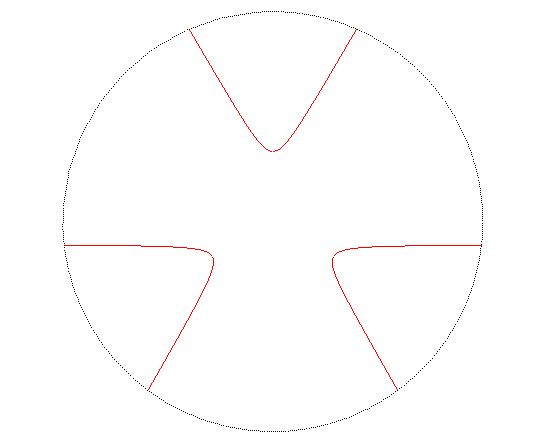
TRÈFLE ÉQUILATÈRE
Equilateral
trefoil, Gleichseitiges Dreiblatt
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
TRÈFLE ÉQUILATÈRE
Equilateral
trefoil, Gleichseitiges Dreiblatt
| Courbe étudiée par G.
de Longchamps en 1884.
Autre nom : trisectrice de Longchamps. |
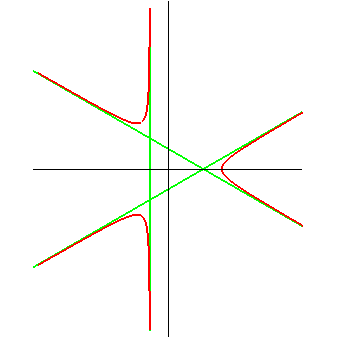
Les asymptotes forment un triangle équilatéral. |
Équation polaire :  .
Équation cartésienne : 
ou  .
(nota : (0,0) est un point isolé de la courbe algébrique). Paramétrisation cartésienne : 
( ).
Cubique rationnelle à point isolé (O). |
Le trèfle équilatère est :
- un épi à trois branches
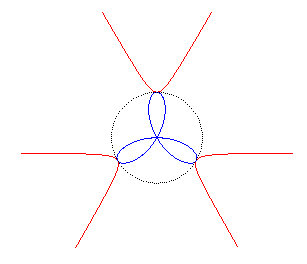
| - l'inverse
du trifolium régulier
par rapport à son centre
|
 |
| - donc ausi la polaire réciproque de l'antipodaire du trifolium, à savoir la deltoïde |  |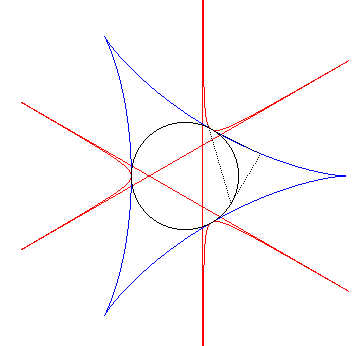
- la courbe obtenue comme lieu des
points d'intersection de deux tangentes en P et Q à
un cercle de centre O, l'angle 
étant le double de  .
Explication : la droite (PQ) enveloppe la deltoïde, polaire du trèfle. |
 |
et de la droite 
(à vérifier !!!!!) (voir à cissoïdale
de Zahradnik).
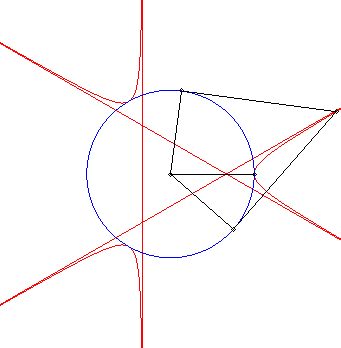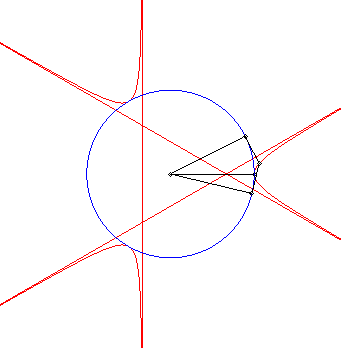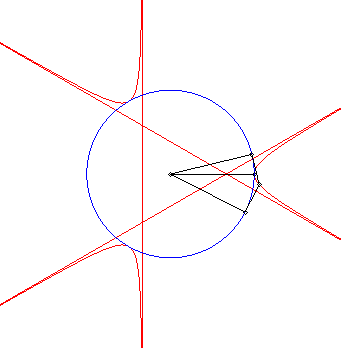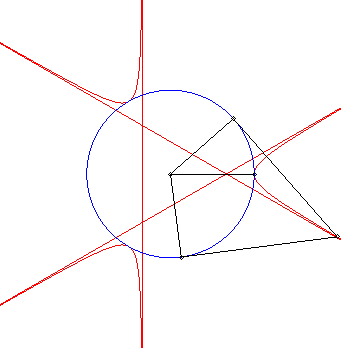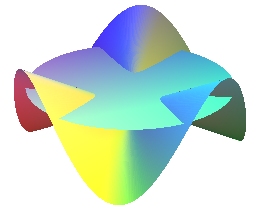
| - la section plane d'un cône sinusoïdal |
 |
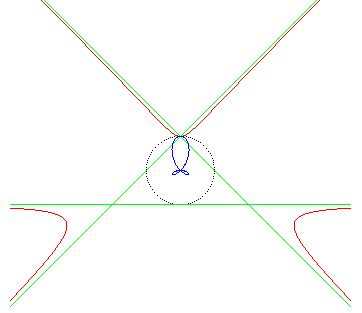
Comme son deuxième nom l'indique, c’est une trisectrice.
|
Cette courbe est assez proche de la courbe d'équation polaire 
(inverse de la torpille) , d'équation
cartésienne : 
ou encore  ,
dont les asymptotes forment cette fois un triangle rectangle isocèle. |
 |
Idem pour la courbe d'équation polaire  ,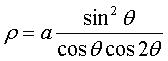
d'équation cartésienne 
ou encore  . |
 |
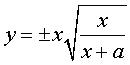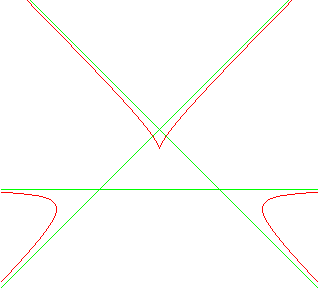Le trêfle équilatère et la cubique
de Humbert (de forme similaire, mais dont les asymptotes sont concourantes)
sont les seules cubiques ayant une symétrie de rotation d'ordre
3 (voir à courbe de Goursat).
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2012